Análise de covariância
Acompanhamento da aula da Professora Fernanda, publicada no dia 14/7/20 no Youtube:
https://www.youtube.com/watch?v=EyqkuCNgj2Y&ab_channel=FernandaPeres
dados <- data.frame(
stringsAsFactors = T,
Sujeito = c(1L,2L,3L,4L,5L,6L,7L,8L,
9L,10L,11L,12L,13L,14L,15L,16L,17L,18L,19L,
20L,21L,22L,23L,24L,25L,26L,27L,28L,29L,30L),
Gênero = c("M","F","M","M","F","F",
"M","M","M","M","F","F","F","F","F","M","M","M",
"F","M","M","F","F","F","M","F","F","M","M",
"F"),
Grau_Instrução = c("Superior","Superior",
"Superior","Ens Fundamental","Ensino Médio","Superior",
"Ens Fundamental","Superior","Superior","Ensino Médio",
"Superior","Ensino Médio","Ensino Médio","Ensino Médio",
"Ensino Médio","Superior","Superior","Superior",
"Ensino Médio","Ensino Médio","Ens Fundamental",
"Ens Fundamental","Ensino Médio","Superior","Ensino Médio",
"Ens Fundamental","Superior","Ens Fundamental","Superior",
"Superior"),
n_Filhos = c(1L,0L,0L,0L,0L,2L,0L,0L,
1L,2L,0L,3L,0L,0L,1L,1L,0L,0L,2L,2L,2L,0L,
0L,2L,4L,1L,1L,0L,0L,1L),
Idade = c(31L,25L,33L,20L,23L,37L,
38L,37L,34L,40L,41L,46L,26L,41L,43L,27L,26L,42L,
43L,30L,35L,33L,30L,32L,29L,40L,36L,34L,31L,
35L),
Salário = c(8.2,5.3,9.4,2.9,3.7,4.4,
4.7,5.4,5.8,3.2,6,6.9,2,3.4,3.7,4.2,6.4,11.6,
8.6,5.5,6.8,4.1,4.6,6.6,7.3,7.3,8.3,3.8,6.2,8)
)summary(dados)## Sujeito Gênero Grau_Instrução n_Filhos Idade
## Min. : 1.00 F:15 Ens Fundamental: 6 Min. :0.0000 Min. :20.00
## 1st Qu.: 8.25 M:15 Ensino Médio :10 1st Qu.:0.0000 1st Qu.:30.00
## Median :15.50 Superior :14 Median :0.5000 Median :34.00
## Mean :15.50 Mean :0.8667 Mean :33.93
## 3rd Qu.:22.75 3rd Qu.:1.7500 3rd Qu.:39.50
## Max. :30.00 Max. :4.0000 Max. :46.00
## Salário
## Min. : 2.000
## 1st Qu.: 4.125
## Median : 5.650
## Mean : 5.810
## 3rd Qu.: 7.200
## Max. :11.600Neste exemplo, queremos analisar se o grau de instrução desses indivíduos tem efeito sobre os salários, controlando esse efeito pela idade.
Mas, primeiro, vamos analisar os pressupostos de uma análise de covariância. Neste banco temos como variável dependente a variável Salário, variável independente Grau de instrução e como covariável idade:
1 - vamos verificar se há efeito da variável independente sobre a covariável:
iniciamos com nossa hipótese nula \(H_0\): não há efeito da variável independente na covariável (p>0,05).
summary(aov(Idade ~ Grau_Instrução, data = dados))## Df Sum Sq Mean Sq F value Pr(>F)
## Grau_Instrução 2 20.4 10.21 0.227 0.799
## Residuals 27 1215.4 45.02Dessa forma, temos evidência para não rejeitar \(H_0\) e constatar que não há efeito do grau de instrução na idade.
2 - verificar se a relação entre a covariável e a variável dependente é linear (VD ~ cov)
ggplot2::ggplot(
dados,
ggplot2::aes(
x = Idade,
y = Salário,
group = Grau_Instrução,
color = Grau_Instrução
)
) +
ggplot2::geom_point(size = 2) +
ggplot2::geom_smooth(method = "lm", se = F, size = .5)## Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
## ℹ Please use `linewidth` instead.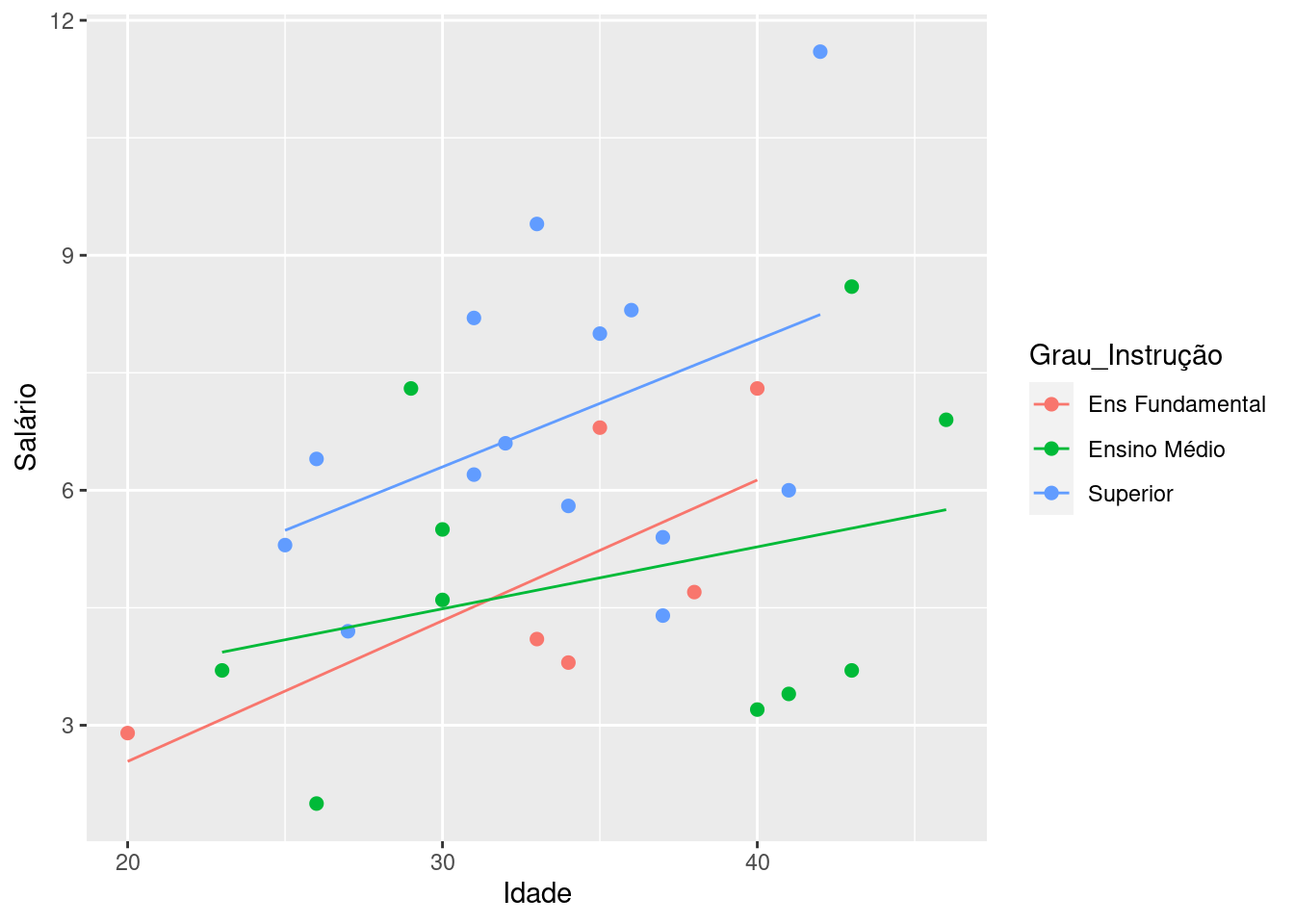
3 - verificar se o efeito da covariável e o mesmo para todos os níveis da variável independente (VD ~ VI * cov). Vamos comparar as inclinações das retas para cada grupo da VI. Ou seja, se houver homogeineidade nos parâmetros da regressão, observaremos retas com inclinações parecidas.
summary(aov(Salário ~ Grau_Instrução*Idade, dados))## Df Sum Sq Mean Sq F value Pr(>F)
## Grau_Instrução 2 28.01 14.005 3.779 0.0374 *
## Idade 1 18.47 18.470 4.984 0.0352 *
## Grau_Instrução:Idade 2 2.52 1.261 0.340 0.7150
## Residuals 24 88.95 3.706
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1car::Anova(aov(Salário ~ Grau_Instrução*Idade, dados), Type = "III")## Anova Table (Type II tests)
##
## Response: Salário
## Sum Sq Df F value Pr(>F)
## Grau_Instrução 31.968 2 4.3130 0.02511 *
## Idade 18.470 1 4.9836 0.03518 *
## Grau_Instrução:Idade 2.522 2 0.3402 0.71501
## Residuals 88.946 24
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1É necessário que a interação entre grau de instrução e idade não seja significativo. Neste teste, vamos ter a \(H_0\) de que há homogeneidade dos parâmetros da regressão (p > 0.05).
4 - Verificar se há homogeneidade de variâncias (VD ~ VI)
car::leveneTest(Salário ~ Grau_Instrução, center = mean, dados)## Levene's Test for Homogeneity of Variance (center = mean)
## Df F value Pr(>F)
## group 2 0.1854 0.8318
## 27Temos que a \(H_0\) é que as variâncias são homogêneas (P>0.05).
5 - Ajustar o modelo de ANCOVA (VD ~ cov + VI)
car::Anova(aov(Salário ~ Idade + Grau_Instrução, data = dados), type = "III")## Anova Table (Type III tests)
##
## Response: Salário
## Sum Sq Df F value Pr(>F)
## (Intercept) 0.629 1 0.1787 0.67596
## Idade 18.470 1 5.2501 0.03030 *
## Grau_Instrução 31.968 2 4.5436 0.02031 *
## Residuals 91.467 26
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Temos que a \(H_0\) é que não há efeito (p >.05). Neste caso, temos o efeito do grau de instrução controlado pela idade.
6 - Verificar a normalidade dos resíduos
shapiro.test(aov(Salário ~ Idade + Grau_Instrução, data = dados)$residuals)##
## Shapiro-Wilk normality test
##
## data: aov(Salário ~ Idade + Grau_Instrução, data = dados)$residuals
## W = 0.96498, p-value = 0.4122No teste de shapiro, temos que a \(H_0\) define a distribuição do dados como normal (p >0.05).
7 - Verificar se há homocedasticidade e outliers:
boxplot(aov(Salário ~ Idade + Grau_Instrução, data = dados)$residuals)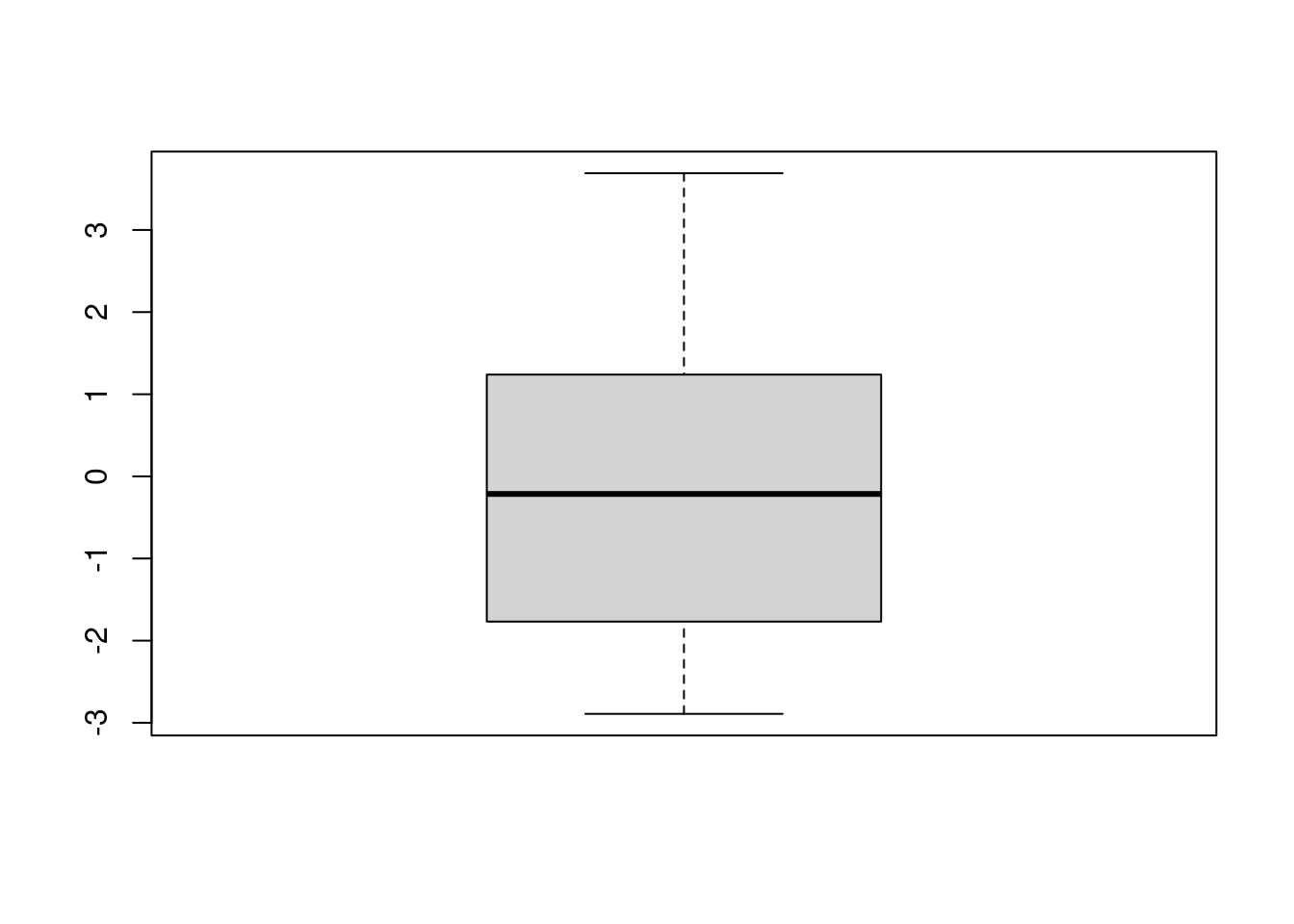
plot(aov(Salário ~ Idade + Grau_Instrução, data = dados), which = 1)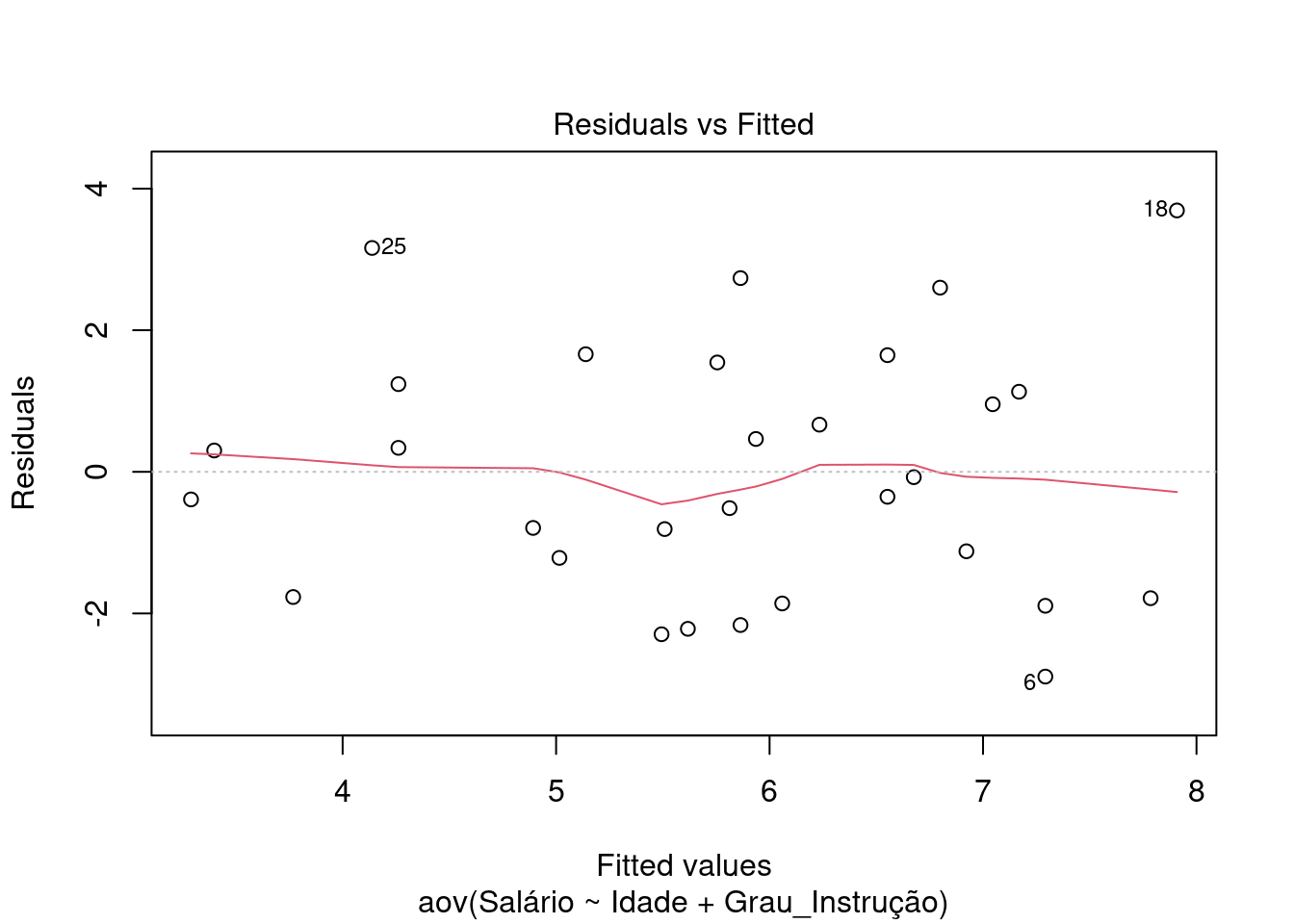
Neste gráfico vemos a distribuição dos resíduos. Se houver homocedasticidade (variância constante), veremos um padrão disperso (talvez mais retangular) dos resíduos. Quando o contrário, veríamos um funil.
Finalizo aqui os ensinamentos da Profa. Fernanda e espero que seja útil para vocês.
Bom trabalho!
